
Dwumienne logo Profesora Goulda pochodzące z książki
Combinatorial Identities

Encyklopedia ciągów liczbowych
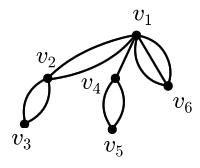
Porządkowe multidrzewo
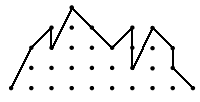
Ścieżka kratowa
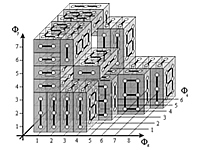
Parkietaż wielowymiarowy
Kombinatoryka
Funkcje tworzące:
- Ściągawka - lista podstawowych własności współczynników dwumiennych, funkcje tworzące etc.
- Równania rekurencyjne o stałych współczynnikach, rodzina ciągów C-skończonych.
- Równanie trzeciego stopnia - funkcja tworząca spełniająca równanie trzeciego stopnia, wyprowadzenie wzoru jawnego, inwersyjne twierdzenie Lagrangea, na przykładzie zliczania ścieżek kratowych.
- Kernel method - metoda wspomagająca poszukiwanie funkcji tworzącej wielu zmiennych.
- Pochodna logarytmiczna - metoda znajdująca równanie rekurencyjne dla ciągu opisanego funkcją tworzącą.
- Generating Functions' Examples - przykłady ciekawych zadań z wykorzystaniem funkcji tworzących, związek ze zredukowanymi algebrami incydencji.
- Liczby Bella i Wzór Dobinskiego - wyprowadzenie wzoru jawnego przy pomocy funkcji tworzących.
Inne:
- Zliczanie podziałów liczb - wprowadzenie, podstawowe rezultaty teorii podziału liczb.
- Argument wielomianowy - metoda, która pozwala uogólniać zbiory argumentów dla tożsamości opisanych wielomianami.
- Zasada włączania-wyłączania - krótkie wprowadzenie i dwa przykłady: wyprowadzenie liczby suriekcji i nieporzadków.
- Problem podziału wielowymiarowych pudełek
- Counting lattice paths - rozprawa doktorska, promotor: prof. dr hab. Andrzej Szepietowski.
Materiały Profesora Andrzeja Krzysztofa Kwaśniewskiego:
Materiały dr Ewy Krot-Sieniawskiej:
Literatura polskojęzyczna:
- Kenneth A. Ross, Charles R.B. Wright. Matematyka dyskretna, Wydanie trzecie, PWN, 2013.
- Ronald L. Graham, Donald E. Knuth, Oren Patashnik. Matematyka konkretna, Wydanie czwarte, PWN, 2013.
- Palka Zbigniew, Ruciński Andrzej. Wykłady z kombinatoryki. WNT, Wydanie drugie, 2009.
- Witold Lipski, Wiktor Marek. Analiza kombinatoryczna, PWN, 1986.
Literatura angielskojęzyczna:
- George E. Andrews. The Theory of Partitions. Encycl. Math. Appl. Vol. 2. Addison-Wesley, Reading, 1976.
- Louis Comtet. Advanced Combinatorics: The Art of Finite and Infinite Expansions. D. Reidel Publishing Company, Boston, U.S.A., 1974.
- Philippe Flajolet and Robert Sedgewick. Analytic Combinatorics. Cambridge University Press, 2009.
- M. Kauers and P. Paule. The Concrete Tetrahedron. SpringerWienNewYork, 2011.
- George E. Martin. Counting: The Art of Enumerative Combinatorics. Undergraduate Texts in Mathematics. Springer, 2001.
- A. Nijenhuis, H. S. Wilf. Combinatorial Algorithms, Academic Press, 1976.
- Richard P. Stanley. Enumerative Combinatorics, volume I (2011), II (2001). Cambridge University Press.
- Herbert S. Wilf. Generatingfunctionology. Academic Press, 1994.