Pamięci Profesora Andrzeja Krzysztofa Kwaśniewskiego (1947-2011)
Gian Carlo Rota Polish Seminar
Gian Carlo Rota Polish Seminar *
| prowadzący: | a.k.kwaśniewski |
| the member of the | Institute of Combinatorics and its Applications |
| Editorial Committee Member in | Advanced Studies in Contemporary Mathematics |
| Editorial Board Member of | JOURNAL OF ANALYSIS AND APPLICATIONS (INDIA) |
Fibonacci Number Theorists
| data | autor | tytuł |
|---|---|---|
| April 2008 | A.K.Kwasniewski, M. Dziemiańczuk | On cobweb posets most relevant codings |
|
Abstract One considers here orderable acyclic digraphs named KoDAGs which represent the outmost general chains of dibicliques denoting thus the outmost general chains of binary relations. Because of this fact KoDAGs start to become an outstanding concept of nowadays investigation. We propose here examples of codings of KoDAGs looked upon as infinite hyper-boxes as well as chains of rectangular hyper-boxes in $N^\infty$. Neither of KoDAGs codings considered here is a poset isomorphism with $\Pi = \langle P, \leq\rangle$ . Nevertheless every example of coding supplies a new view on possible investigation of KoDAGs properties. The codes proposed here down are by now recognized as most relevant codes for practical purposes including visualization. More than that. Employing quite arbitrary sequences $F=\{n_F\}_{n\geq 0}$ infinitely many new representations of natural numbers called base of F number system representations are introduced. These constitute mixed radix-type numeral systems. F base nonstandard positional numeral systems in which the numerical base varies from position to position have picturesque interpretation due to KoDAGs graphs and their correspondent posets which in turn are endowed on their own with combinatorial interpretation of uniquely assigned to KoDAGs F-nomial coefficients. The base of F number systems are used for KoDAGs coding and are interpreted as chain coordinatization in KoDAGs pictures as well as systems of infinite number of boxes sequences of F-varying containers capacity of subsequent boxes. Needless to say how crucial is this base of F number system for KoDAGs hence consequently for arbitrary chains of binary relations. New F based numeral systems are umbral base of F number systems in a sense to be explained in what follows. AMS Classification Numbers: 06A07, 05C78, 11A63; 23 pages, 15 figures, Bibliography [1] A. K. Kwaśniewski, M. Dziemiańczuk On cobweb posets most relevant codings arXiv:math.CO/0804.1728, Thu, 10 Apr 2008 06A07 Combinatorics of partially ordered sets 05C78 Graph labelling 11A63 Radix representation; digital problems Mixed radix numeral systems are non-standard positional numeral systems in which the numerical base varies from position to position. ad MS Classification 2000 http://www.ams.org/msc/classification.pdf |
||
| March 2008 | Wiesław Bajguz | More on Algebraic Structure of the Complete Partition Function for the Zn - Potts Model |
|
Abstract In this first part of a larger review undertaking the results of the firstauthor and a part of the second author doctor dissertation are presented. Nextwe plan to give a survey of a nowadays situation in the area of investigation.Here we report on what follows. Calculation of the partition function for anyvector potts model is at first reduced to the calculation of traces of productsof the generalized clifford algebra generators. The formula for such traces isderived. This enables one, in principle, to use an explicit calculation algorithm forpartition functions also in other models for which the transfer matrix is anelement from generalized clifford algebra. The method - simple for Z2 case - becomes complicated for Zn, n>2,however everything is controlled , in principle, due to knowledge of thecorresponding algebra properties and those of generalized cosh function. Thediscussion of the content of the in statu nascendi second part is to be foundat the end of this presentation. This constitutes the last section. Bibliography [1] A. K. Kwaśniewski , W. Bajguz, More on Algebraic Structure of the Complete Partition Function for the Zn - Potts Model, Part 1, arXiv: 0803.1305, Sun, 9 Mar 2008, submitted to Rep. Math. Phys.Categories: math.GM math-ph math.MP, Comments: 23 pages, MSC-class: 11E88, 15A66 [2] W. Bajguz; W.Bajguz PhD dissertation |
||
| March 2008 | A.K. Kwaśniewski | Further broadening of incidence algebra horizon - an informal introduction. Part I |
|
Part I On further Applications if Incidence Algebras description of Posets - QM and all that 1] at first - comments on \bibitem {xx}Vladimir V. Kisil , {\it The Umbral Calculus and Cancellation Semigroup Algebras} Zeitschrift für Analysis und ihre Anwendungen, {\bf 19} no. 2, (2000), 315-338.E-print: arXiv:funct-an/9704001.See page 6 „Our agreement is equivalent to introduction of incidence algebra of …”[knowledge of QM - not needed]then 2] a look on relevant Roman R. Zapatrin's contribution knowledge of QM - not at the first stage obligatory however a bit of QM - recommended,then gradually - more and more 3] goal? how are doing KoDAGs with all this- being so much around? 4] Aristophanes Dimakis? and discrete space time history... Bibliography [1] Vladimir V. Kisil [2] Roman R. Zapatrin [3] Aristophanes Dimakis |
||
| January- February 2008 | Ewa Krot-Sieniawska | On Incidence Algebras of Cobweb Posets |
|
in Polish Przedstawię najnowsze wyniki własne dotyczące opisu algebrami incydencji całej bez wyjątków rodziny „cobweb posetów” - rodziny odkrytej i wprowadzonej do matematycznych podstaw informatyki kilka lat temu przez autora [1]. Używam definicji tych digrafów Kwaśniewskiego tak jak np. w [1] z 2007 roku. Pojawia się tu w [1] i nowa znamienna charakteryzacja a zatem definicja owych cobweb posetów poprzez tym szczególny typ diagramu Hasse , że stanowi go DAG niejako „matkujący” wszystkim z rodziny grafów łańcuchów relacji - grafów łańcuchów wszelkich relacji binarnych. Podkreślmy – WSZELKICH! Patrz [1]. Fakt ten stanowi o wyjątkowej roli rozważanego typu KoDAG grafów [KoDAG = Kwaśniewski-oDAG] W pierwszej części wyprowadzone będą wzory jawne na:
legenda oDAG = orderable Directed Acyclic Digraph - patrz np. [3] i prace Profesora Bibliography [1] A. Krzysztof Kwaśniewski On cobweb posets and their combinatorially admissible sequences, arXiv:math.CO/0512578 v1 26 Dec 2005 - 21 Oct 2007. [2] E.Krot-Sieniawska Rozszerzenia Rachunku operatorowego Roty I pokrewne zastosowania analizy kombinatorycznej, przygotowywana praca doktorska [3] E. Krot The first ascent into the Fibonacci Cob-web Poset, Advanced Studies in Contemporary Mathematics 11 (2005), No. 2, pp.179-184, ArXiv: math.CO/0411007 [4] Spiegel E., O`Donnell Ch. J. Incidence algebras, Marcel Dekker, Inc. Basel 1997 [5] Stanley R. P. Enumerative Combinatorics, Volume I, Wadsworth\& Brooks/ColeAdvanced Books \& Software, Monterey California, 1986 [6] Anatoly Plotnikov's Publications http://www.vinnica.ua/~aplot/publicat.htmla
| ||
| January 2008 | Maciej Dziemiańczuk | On Cobweb admissible sequences- The Production Theorem |
|
In English Further [1] clue decisive observations on cobweb admissible sequences are shared with the audience. In particular an announced proof of the Theorem 1 (by Dziemiańczuk) from [1] announced in India –Kolkata- December 2007 is delivered here. Namely here and there we claim that any cobweb admissible sequence F is at the point product of primary cobweb admissible sequences taking values one and/or certain power of an appropriate primary number p. Here one delivers also the so much desired [2,3,1] algorithm to produce the family of all cobweb-admissible sequences i.e. the Problem 1 from [1] problems posed in source papers [2,3] is solved using the idea and methods implicitly present already in [4]. Bibliography [1] A. Krzysztof Kwaśniewski, M. Dziemiańczuk, Cobweb posets – Recent Results; ISRAMA Congress; December 15-17 2007 Kolcata, INDIA see ArXiv [2] A. Krzysztof Kwaśniewski, Cobweb posets as noncommutative prefabs Adv. Stud. Contemp. Math. vol. 14 (1) (2007) 37-47. [3] A. Krzysztof Kwaśniewski, On cobweb posets and their combinatorially admissible sequences, arXiv:math.CO/0512578 v1, 26 Dec 2005, 21 Oct 2007. [4] Maciej Dziemiańczuk On Cobweb posets tiling problem arXiv:0709.4263, 4 Oct 2007 | ||
| November 2007 | Ewa Krot-Sieniawska | On Characteristic polynomials of Cobweb Posets |
A graded poset, sometimes called a ranked poset, is a partially ordered set (poset) P in which every maximal chain is finite and has the same length. Every graded poset has an integer-valued rank function.
Equivalently, a poset P is graded if it admits a partition into maximal antichains An for n = 0, 1, ..., r (where r is a nonnegative integer) such that for each x being an element of An, all of the elements covering x are in An + 1 and all the elements covered by x are in An - 1. The rank of P, written ?(P), is the maximum rank of any element. The rank of a minimal element is 0.
A finite graded poset P with a unique minimal element (called 0) has an important invariant called its characteristic polynomial. Let µ be the Möbius function of P. The characteristic polynomial of P is 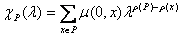 Examples of graded posets are the so called (Kwaśniewski’s) Cobweb Posets defined in [3,4]. Following the expression for the Möbius function of Fibonacci and other cobweb posets from [5] the family of characteristic polynomials of these structures will be presented. in Polish Zbiór częściowo uporządkowany P nazywamy posetem z rangą, jeśli w dowolnym jego odcinku wszystkie łańcuchy maksymalne są tej samej długości. Rangą ?(x) elementu x z P nazywamy wówczas długość łańcucha maksymalnego łączącego element najmniejszy (ew. minimalny) z x. Dla takiego zbioru P możemy określić jego wielomian charakterystyczny następująco: Jeśli µ jest funkcją Möbiusa posetu P, to Przykładami posetów z gradacją są zdefiniowane przez Kwaśniewskiego m.in. w [3,4], tzw. cobweb posety. Pokażę znane [1,2,7] przykłady posetów z rangą i ich wielomiany charakterystyczne, a także przykłady zastosowań tychże wielomianów. Korzystając z postaci funkcji Möbiusa dla Fibonacci cobweb posetu z [5], reprezentatywnej dla całej rodziny tych struktur, wyprowadzę wielomiany charakterystyczne dla cobweb posetów Bibliography [1] B. Sagan, Why the characteristic polynomial factors, Bull. Amer. Math. Soc. 36 (1999), 113–134. [2] B. Sagan, M¨obius Functions of Posets IV: Why the Characteristic Polynomial Factors , www.math.msu.edu/~sagan/Slides/mfp4.pdf [3] A. Krzysztof Kwaśniewski, Cobweb posets as noncommutative prefabs Adv. Stud. Contemp. Math. vol. 14 (1) (2007) 37-47 [4] A. Krzysztof Kwaśniewski, On cobweb posets and their combinatorially admissible sequences, arXiv:math.CO/0512578 v1 26 Dec 2005. [5] E. Krot, The first ascent into the Fibonacci Cob-web Poset, Advanced Studies in Conterporary Mathematics 11 (2005), No. 2, pp.179-184, ArXiv: math.CO/0411007 [6] http://en.wikipedia.org/wiki/Graded_poset [7] Joni S. A., Rota. G.-C., Sagan B. From Sets to Functions: Three Elementary Examples, Discreta Mathematics 37 (1981) pp.193-202 | ||
| December 2007 | Maciej Dziemiańczuk | On cobweb-admissibility characterization |
|
I shall present some observations on cobweb admissible sequences.
Among others a proof is given of the statement:
Any cobweb admissible sequence F is at the point product of cobweb admissible sequences primary numbers valued by one and/or a certain primary number p.
I shall also disclose family of all such primary cobweb admissible sequences in a form of the corresponding binary tree. As for the background see the source papers [1,2,3].
Abstrakt a) pokażę, iż można każdy cobweb admissible ciąg przedstawić za pomocą iloczynu w punkcie prostych ciągów składających się z wartości {1, p}, gdzie p to liczba pierwsza b) ujawnię opis wszystkich takich prostych ciągów za pomocą nieskończonego poddrzewa drzewa binarnego Bibliography [1] A. Krzysztof Kwaśniewski, Cobweb posets as noncommutative prefabs Adv. Stud. Contemp. Math. vol. 14 (1) (2007) 37-47 [2] A. Krzysztof Kwaśniewski, On cobweb posets and their combinatorially admissible sequences, arXiv:math.CO/0512578 v1 26 Dec 2005. [3] Maciej Dziemiańczuk On Cobweb posets tiling problem arXiv:0709.4263 | ||
| November 2007 | Maciej Dziemiańczuk | On cobweb tilings algorithms |
|
We present some of cobweb tilings algorithms for searching all the partitions of any layer and their computational complexity as rough upper bounds of cobweb tiling problem. We show also that rough upper bound of tiling problem can be smaller than that which was introduced in [2] a month ago. This is a continuation of [6].
Bibliography [1] A. Krzysztof Kwaśniewski, Cobweb posets as noncommutative prefabs Adv. Stud. Contemp. Math. vol. 14 (1) (2007) 37-47 [2] A. Krzysztof Kwaśniewski, On cobweb posets and their combinatorially admissible sequences, arXiv:math.CO/0512578 v1 26 Dec 2005. [3] Ewa Krot, An Introduction to Finite Fibonomial Calculus, Central European Journal of Mathematics 2(5) (2005) 754-766 [4] A. Krzysztof Kwaśniewski Main theorems of extended finite operator calculus Integral Transforms and Special Functions Vol. 14, No 6 (2003) 499-516. [5] A.Krzysztof Kwaśniewski The logarithmic Fib-binomial formula Advan. Stud. Contemp. Math. v.9 No.1 (2004) 19-26. [6] Maciej Dziemiańczuk On Cobweb posets tiling problem arXiv:0709.4263 [7] Eduard Lucas Théorie des Fonctions Numériques Simplement Périodiques American Journal of Mathematics Volume 1 (1878), pp. 184-240 (Translated from the French by Sidney Kravitz, Edited by Douglas Lind Fibonacci Association 1969 | ||
| October 2007 | Maciej Dziemiańczuk | On Cobweb posets tiling problem |
|
Kwaśniewski`s cobweb posets uniquely represented by directed acyclic graphs are such a generalization of the Fibonacci tree that allows joint combinatorial interpretation for all of them under admissibility condition. This interpretation was derived in the source papers and it entailes natural enquieres already formulated therein. In our note we response to one of those problems. This is a tiling problem. Our observations on tiling problem include proofs of tiling’s existence for some cobweb-admissible sequences. We show also that not all cobwebs admit tiling as defined below.
Bibliography [1] A. Krzysztof Kwaśniewski, Cobweb posets as noncommutative prefabs Adv. Stud. Contemp. Math. vol. 14 (1) (2007) 37-47 [2] A. Krzysztof Kwaśniewski, On cobweb posets and their combinatorially admissible sequences, arXiv:math.CO/0512578 v1 26 Dec 2005. [3] Ewa Krot, An Introduction to Finite Fibonomial Calculus, Central European Journal of Mathematics 2(5) (2005) 754-766 [4] A.Krzysztof Kwaśniewski, Main theorems of extended finite operator calculus Integral Transforms and Special Functions Vol. 14, No 6 (2003) 499-516. [5] A.Krzysztof Kwaśniewski The logarithmic Fib-binomial formula Advan. Stud. Contemp. Math. v.9 No.1 (2004) 19-26. [6] Maciej Dziemiańczuk, [7] Eduard Lucas Théorie des Fonctions Numériques Simplement Périodiques American Journal of Mathematics Volume 1 (1878), pp. 184-240 (Translated from the French by Sidney Kravitz, Edited by Douglas Lind Fibonacci Association 1969 | ||
| March - April 2007 | Ewa Krot-Sieniawska | On Combinatorial Species |
The central concept of the combinatorial theory is to enumerate discrete structures, i.e.: permutations, graphs, trees, derangements and so on. Each of these has an associated generating function (formal series) which counts how many structures there are of the certain size. We are able to analyse complicated structures by describing them in terms of transformations and combinations of simpler structures. These operations correspond to equivalent manipulations of generating functions. The Category Theory provides the tools to give a proper mathematical foundation to our combinatorial intuition trough this concept - The Theory of Combinatorial Species introduced by Andre Joyal in 1981.
It is an abstract, systematic method for analyzing discrete structures (for example) in terms of generating functions. A combinatorial object (species) is a functor from the category B of finite sets and bijections to itself. To each species S one associates its exponential generating series
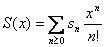 ,
where sn is the cardinality of set of S- structures on any set with n elements. Certain “natural” operations on species, for example addition, multiplying (product), composition (substitution ), differentiation and so on correspond to some operations on generating functions.
I’ll give basic definitions of the theory and some examples of their settings. ,
where sn is the cardinality of set of S- structures on any set with n elements. Certain “natural” operations on species, for example addition, multiplying (product), composition (substitution ), differentiation and so on correspond to some operations on generating functions.
I’ll give basic definitions of the theory and some examples of their settings.
Bibliography [1] André Joyal, Une théorie combinatoire des séries formelles, Advances in Mathematics 42:1-82 (1981). [2] Francois Bergeron, Gilbert Labelle, Pierre Leroux, Combinatorial Species and Tree-like Structures, Cambridge University Press, Cambridge, 1998. [3] Francois Bergeron, MI>Species and Variations on the theme of Species, invited talk at Category Theory and Computer Science ’04 ( http://www.itu.dk/research/theory/ctcs2004/ ), Copenhagen (2004). Slides (pdf) ( http://bergeron.math.uqam.ca/Especes_trans.pdf ). [4] Federico G. Lastaria, An Invitation to Combinatorial Species, http://math.unipa.it/~grim/ELastaria221-230.PDF [5] http://en.wikipedia.org/wiki/Combinatorial_species | ||
| March 2007 | Wiesław Bajguz | Introduction to category theory |
|
Categories were first introduced by Samuel Eilenberg and Saunders Mac Lane in 1942-1945 as an important part of the transition from homology (an intuitive and geometric concept) to homology theory. Category theory is applied in most branches of mathematics (see – theory of species in combinatorics).
This talk is an introduction to categries. We start with definitions and basic facts from this theory - in the spirit of recollection of the already known to the audience.
Bibliography [1] Z. Semadeni, A.Wiweger, Wstęp do teorii kategorii i funktorów BM 45, PWN, Warszawa 1978 [2] D. Turi Category Theory Lecture Notes http://www.dcs.ed.ac.uk/home/dt/CT/categories.pdf [3] M. M. Fokkinga A Gentle Introduction to Category Theory - the calculational approach , http://wwwhome.cs.utwente.nl/~fokkinga/mmf92b.html [4] Michael Barr and Charles Wells Cathegory theory Lecture Notes http://folli.loria.fr/cds/1999/library/pdf/barrwells.pdf [5] Federico G. Lastaria An Invitation to Combinatorial Species, http://math.unipa.it/~grim/ELastaria221-230.PDF | ||
| February 2007 | a. krzysztof kwaśniewski [Tachion] |
Cardinals, Ordinals, Non-Archimedian Fields and NSA i.e. Infinitezimal and infinite nonstardard numbers |
|
Nonstandard Analysis is a branch of mathematical logic which introduces hyperreal numbers to allow for the existence of genuine infinitesimals.
ANALIZA NIESTANDARDOWA to ział matematyki rozwinięty w latach 60. XX w. przez A. Robinsona, będący ścisłą realizacją pochodzącej z XVII w. koncepcji G.W. Leibniza, który chciał oprzeć cały rachunek różniczkowy i całkowy na pojęciu nieskończenie małej; podstawowym obiektem w analizie niestandardowej jest tzw. ciało liczb hiperrzeczywistych R* (jego podzbiorem są zwykłe liczby rzeczywiste), w którym nie zachodzi aksjomat Archimedesa [0!], tzn. istnieją elementy mniejsze od każdej zwykłej liczby rzeczywistej dodatniej, a mimo to większe od zera; w języku analizy niestandardowej można dokonać rekonstrukcji właściwie całej klasycznej analizy matematycznej- przy czym podanie definicji np. funkcji ciągłej, czy pochodnej funkcji, wymaga mniejszej liczby kwantyfikatorów niż w klasycznym rachunku różniczkowym.
Newton and Leibniz used infinitesimal methods in their development of the calculus, but were unable to make them precise, and Weierstrass eventually provided the formal epsilon-delta idea of limits.
Abraham Robinson developed nonstandard analysis in the 1960's, and the theory has since been investigated for its own sake, and has been applied in areas such as Banach spaces, differential equations, probability theory, microeconomic theory and mathematical physics.
Nonstandard analysis is also sometimes referred to as infinitesimal analysis. Basic notions and ideas underlying the presentation are to be found in [1,6].
Bibliography [0!] J. Browkin Teoria ciał PWN, Warszawa 1978 [patrz Rozdział IV, §1 ] [1] E. Nelson Internal set theory: A new approach NonStardard Analysis Bull. Amer. Math. Soc., 83(6):1165–1198, 1977 [2] E. Nelson Confessions of an apostate mathematician debate with Ennio De Giorgi, Forl`i, Italy, 1995. http://www.math.princeton.edu/~nelson/papers.html [3] E. Nelson Mathematics and faith in “The Human Search for Truth: Philosophy, Science, Theology– The Outlook for the Third Millennium” International Conference on Science and Faith,The Vatican, 23-25 May 2000, St. Joseph’s University Press, Philadelphia, 2002 http://www.math.princeton.edu/~nelson/papers.html [4] E. Nelson Completed versus incomplete infinity in arithmetic, presented to STOQ International Con-ference on Infinity in Science, Philosophy, and Theology, Pontifical Lateran University, Vatican City, November 9–11, 2005. http://www.math.princeton.edu/~nelson/papers.html [5] E. Nelson Syntax and semantics, presented to International Conference: “Foundations and the Onto-logical Quest. Prospects for the New Millennium”, Pontifical Lateran University, Vatican City, January 7–10, 2002. http://www.math.princeton.edu/~nelson/papers.html [6] H. Jerome Keisler Elementary Calculus An Approach Using Infinitesimals. First edition 1976; 2nd edition 1986 in pdf format available for downloading at http://www.math.wisc.edu/~keisler/calc.html | ||
| May 2006 | Dominique Foata, Guo Niu Han przedstawia: A.K.Kwasniewski, W.Bajguz, E. Krot-Sieniawska |
Nombres de Fibonacci et polynomes orthogonaux |
|
RÉSUMÉ : Le calcul des séries de produits de nombres de Fibonacci et des polynômes de Tchebicheff des deux especes
est obtenu ici a l`aide de deux méthodes combinatoires.
Bibliography [1] Dominique Foata, Guo Niu Han Nombres de Fibonacci et polynômes orthogonaux in Leonardo Fibonacci: il tempo, le opere, l'ereditá scientifica [Pisa. 23-25 Marzo 1994, Marcello Morelli e Marco Tangheroni, ed.], p. 179-200. Pisa, Pacini Editore (Fondazione IBM Italia), 1994. www-irma.u-strasbg.fr/~foata/paper/pub71.html [2] see references in [1] above | ||
| April 2006 | Ewa Borak | Partition Statistics and q-Bell Numbers |
|
Following Carl G. Wagner [1] tree q-generalization of Stirling numbers of second kind will be presented. These q-Stirling numbers are generating functions for three statistics on the set of partitions of [n] with k blocks. The unified treatment of these numbers will be presented.
Bibliography [1] Carl G. Wagner: "Partition Statistics and q-Bell Numbers (q=-1)" Journal of Integer Sequences, Vol. 7 (2004), Article 04.1.1 | ||
| April 2006 | Ewa Krot-Sieniawska | Generalized Stirling and Lah numbers |
|
Following Carl G. Wagner [1,2] three generalizations of Stirling numbers of the second kind, and of Lah numbers are presented. Combinatorial interpretation of these generalizations will be given by the use of the theory of modular binomial lattices [3].
Bibliography [1] C.G Wagner: Generalized Stirling and Lah numbers, Discrete Mathematics, 160 (1996), pp.199-218 [2] C.G.Wagner: Suriections, Differences, and Binomial Lattices, Studies In Applied Mathematics, 93 (1994), pp.15-27 [3] P.Doubilet, G.-C. Rota, R.Stanley: On the Foundations of Combinatorial Theory VI:The Idea of Generating Functions, In 6th Berkeley Symp. Math. Stat. Prob. vol. 2 (1972), pp. 267-318 | ||
| March 13, April 2006 | A.K.Kwaśniewski przedstawia: E. Borak |
On umbral extensions of Stirling numbers and Dobinski-like formulas |
|
Stirling numbers of the second kind are umbrally extended in a new way and the resulting new type of dobinskian formulae are discovered. These extensions naturally encompass the well known extensions. The fact that the q-umbral extended dobinskian formulae may also be interpreted as the average of powers or polynomials of specific random variable with the extended Poisson like distribution singles out the q-extensions which appear to be a kind of bifurcation point in the domain of umbral extensions. Because of this the Because of this the further consecutive umbral extensions are here realized in a twofold way.
Bibliography [1] A.K. Kwaśniewski On umbral extensions of Stirling numbers and Dobinski-like formulas submitted - under correction 2005, ArXiv: math.CO/0503286 2005 [2] see references in [1] above | ||
| February 2006 | Wiesław Bajguz | Graphs compositions |
|
New results in compositions of unions of graphs shall be presented.
The author shall define such a chain of graphs, which is a generalization of ladders and will
demonstrate his method of counting of these. Basic notions and ideas underlying the presentation are to
be found in [1]; see also [2].
Bibliography [1] A. Knopfmacher, M. E. Mays, Graph Compositions I: Basic Enumeration Integers: Electronic Journal of Combinatorial Number Theory. 1 #A04 (2001): 1-11. www.integers-ejcnt.org/vol1.html [2] J. N. Ridley, M. E. Mays Compositions of Unions of Graphs The Fibonacci Quarterly, Vol. 42, No 3 (2004) pp. 222-230. | ||
| 23 January 2006 | Maciej Dziemiańczuk | Remarks on cobweb posets` Kwasniewski Hypothesis and Related Questions posed by [1] |
|
prime cobweb posets
Pn = Cn[F; (F1), (F2),..., (Fn)]
introduced by Kwasniewski in [1] are considered.
Examples are provided in abundance. Hypothesis concerning their combinatorial interpretation by Kwasniewski
is to undergo various attempts of verification along the lines outlined by the author
of the hypothesis and the author of the presentation.
Bibliography [1] A.K. Kwaśniewski On cobweb posets and their combinatorially admissible sequences http://arxiv.org/PS_cache/math/pdf/0512/0512578.pdf 2006 [2] see references in [1] above | ||
| November/December 2005 | A.K. Kwaśniewski | Cobweb posets as noncommutative prefabs |
|
A class of new type graded infinite posets with minimal element are considered. These so called cobweb posets introduced recently by the present author provide a wide range of new noncommutative prefab combinatorial schema with characteristic graded subposets as primes. The schema are defined here via relaxing commutativity and associativity requirements imposed on the composition of prefabs by the fathers of this fertile concept. The construction and the very first basic properties of cobweb prefabs are pointed out in what follows. An another single valued commutative amd associative composision is also considered.
Bibliography [1] A. K. Kwaśniewski Cobweb posets as noncommutative prefabs submitted 2005 (October). ArXiv: math.CO/0503286 2005 [2] see references in [1] above | ||
| November 2005 | A.K. Kwaśniewski przedstawia E. Krot-Sieniawska |
Prefab posets` Whitney numbers |
|
We introduce a natural partial order in structurally natural finite subsets the cobweb prefabs sets recently constructed by the present author. Whitney numbers of the second kind of the corresponding subposet which constitute Stirling-like numbers` triangular array are then calculated and the explicit formula for them is provided. Next - in the second construction - we endow the set sums of prefabiants with such an another partial order that their their bell like numbers include fibonacci triad sequences introduced recently by the present author in order to extend famous relation between binomial newton coefficients and fibonacci numbers onto the infinity of their relatives among which there are also the fibonacci triad sequences and binomial-like coefficients (incidence coefficients included).
Bibliography [1] A. K. Kwaśniewski Prefab posets` Whitney numbers in press 2005 (October). ArXiv: math.CO/0510027 Mon, 3 Oct 2005 [2] see references in [1] above | ||
| October 2005 | Ewa Krot-Sieniawska | The first ascent into the incidence algebra of the Fibonacci cobweb poset |
|
The explicite formulas for möbiusien function and some other important elements of the incidence algebra are delivered. For that to do one uses kwa\'sniewski's construction of his fibonacci cobweb poset in the plane grid coordinate system.
Bibliography [1] E. Krot The first ascent into the incidence algebra of the Fibonacci cobweb poset Advan. Stud. Contemp. Math. The paper is to appear in volume 11 (2), 2005 (October). ArXiv: math.CO/0411007 31 Oct 2004 [2] see references in [1] above | ||
| 17 October 2005 | Wiesław Bajguz | Counting of elements of the composition |
|
The number of compositions of positive integer n is 2n-1 – of course. Let us however try to count various subsets of a composition: compositions with parts each less than N, with m different sizes of parts, palindromic compositions, etc.
The knowledge of recurrences and generating functions can help in counting problems.
We shall start discussing these and related topics.
Bibliography [1] George E. Andrews, Sun T. Soh The Theory of Compositions: IV. Compositions with designated summands, (submitted). [2] Phyllis Chinn, Silvia Heubach, (1,k)-Compositions, Congressus Numerantium 164 (2003), pp. 183-194. [3] A Knopfmacher and M E Mays The sum of distinct parts in compositions and partitions, Bull. Inst. Comb. & Appl. 25 (1999), 66-78. [4] Arnold Knopfmacher, M. E. Mays Compositions with m distinct parts Ars Combinatorica 53 (1999), 111-128. [5] Arnold Knopfmacher, Neville Robbins Compositions with parts constrained by the leading summand, to appear in Ars Combinatoria. | ||
| May 2005 | Ewa Krot | Properties and Applications of Stirling and Bell numbers and their extensions II |
|
Following [1,2] one applies probabilistic argumentation apart from combinatorial one in order to re-derive in that way known results and in order start further applications of Stirling and Bell numbers extensions [3].
Bibliography [1] D.Branson Stirling numbers and Bell numbers: their role in combinatorics and probability The Mathematical Scientist, Vol. 25, pp.1-31, 2000 [2] D. Branson An extension of Stirling numbers The Fibonacci Quarterly, Vol. 34, pp. 213-223, 1996 [3] A.K.Kwaśniewski Information on some recent applications of umbral extensions to discrete mathematics to appear in the Proceedings of the International Symposium on Recent Advances in Mathematics and its Applications (ISRAMA 2004) pp. 18-20, December 2004 Kolkata (Calcutta), INDIA ArXiv: math.CO/0411145 7 Nov 2004 | ||
| May 2005 | A. K. Kwaśniewski, Wiesław Bajguz |
Whitney`s logical expansion and hybrid sets |
|
The formulation of Inclusion – Exclusion Principle by Whitney [1] is being recognized as
the one implicitly introducing the algebra of hybrid sets.
Bibliography [1] Whitney Hassler A logical expansion in mathematics Bull. Amer. Math. Soc. (1932) 38, 572-579 | ||
| March-April 2005 | A. K. Kwaśniewski | Applications diverses de la théorie combinatoire des especes de structures- d`apres Jacques Labelle [1] et André Joyal [2] |
|
Le but du présent cycles des presentations est d`illustrer l`edificacité de la Théorie des especes de structures catégorial par un grand nombres d`examples et de l`appliquer a divers
problemes de denombrement. C`est sont l`application simples aussi bien que les plus avancé. les mots clef : foncteur, ...etc.,...,vertébrés , arborescences, derangeménts, partitions etc. Bibliography [1] J. Labelle, Applications diverses de la théorie combinatoire des especes de structures, Annales des Sciences Mathématiques du Québec, (1983) 7 (1), 59-94. (MR 85d: 05018). http://www.labmath.uqam.ca/~annales/volumes/7-1/PDF/59-94.pdf [2] André Joyal Une théorie combinatoire des séries formelles, Advances in Mathematics, 42, 1981, 1-82. [3] Federico G. Lastaria : An Invitation to Combinatorial Species http://math.unipa.it/~grim/ELastaria221-230.PDF | ||
| March-April 2005 | E. Krot A. K. Kwaśniewski |
Properties and Applications of Stirling and Bell numbers and their extensions I |
|
Following [1,2] one applies probabilistic argumentation apart from combinatorial one in order to re-derive in that way known results and in order start further applications of Stirling and Bell numbers extensions [3].
Bibliography [1] D.Branson. Stirling numbers and Bell numbers: their role in combinatorics and probability The Mathematical Scientist, Vol. 25, pp.1-31, 2000 [2] D. Branson. An extension of Stirling numbers, The Fibonacci Quarterly, Vol. 34, pp. 213-223, 1996 [3] A.K.Kwaśniewski Information on some recent applications of umbral extensions to discrete mathematics to appear in the Proceedings of the International Symposium on Recent Advances in Mathematics and its Applications (ISRAMA 2004) pp. 18-20, December 2004 Kolkata (Calcutta), INDIA ArXiv: math.CO/0411145 7 Nov 2004 | ||
| February-March 2005 | Ewa Borak | Further Remarks on Duality Triads |
|
The notion of duality triads [1] is presented . Several examples are quoted [1,2] . The new properties of duality triads are revealed . These are presented following Matthias Schork’s generalization of [2] in [3] . His possible way of generalization of duality triads to higher order recurrences is to be discussed also.
Bibliography [1] A. K. Kwasniewski On duality triads. Bull. Soc. Sci. Lett. Lodz Ser. Rech. Deform. 53, Ser. Rech.Deform. 42 (2003) pp.11-25. math.GM/0402260 [2] A. K. Kwasniewski The second part of on duality triads' paper Bull. Soc. Sci. Lett. Lodz Ser. Rech. Deform. 53, Ser. Rech.Deform. 42 (2003) pp.25-37. math.GM/0402288 [3] Ewa Borak A note on special duality triads and their operator valued counterparts. math.CO/0411041 8 Nov 2004. [4] Matthias Schork Some remarks on duality triads (draft version- December 2004) | ||
| February 2005 | A. K. Kwaśniewski | Les especes de structures et les operations combinatoires- l`applications simples |
|
C`est la recapitulation et en meme cas une introduction elementaire aux la theory des especes de structures d`apres André Joyal [1] avec quelques
application simples;
(vertébrés , arborescences, derangeménts, partitions etc.)
Bibliography [1] André Joyal Une théorie combinatoire des séries formelles, Advances in Mathematics, 42, 1981, 1-82. [2] Gessel , R. Stanley Algebraic enumerationHandbook of combinatorics (vol. 2) Pages: 1021 - 1061 , 1996 MIT Press Cambridge, MA, USA 10 [3] Mathemagics , Matematyka Dyskretna http://ii.uwb.edu.pl/akk/index.html http://globegate.utm.edu/french/globegate_mirror/vocab.html, http://users.skynet.be/providence/vocabulaire/francais/menu.htm | ||
| January 2005 | Ewa Borak Wiesław Bajguz |
Expressing Benoulli numbers (*) and their extensions via Stirling numbers |
|
Following [1,2] one presents a derivation of - among others- the expression of Benoulli numbers in terms of Stirling numbers of the second kind. This is also in order to investigate possible Stirling numbers extensions being involved [3].
Bibliography [1] M.Kaneko The Akiyama-Tanigawa algorithm for Bernoulli numbers J. Integer Seq. 3 (2000), no. 2, Article 00.2.9, 6 pp. (electronic). Z0982.11009; M2001k:11026 [2] CHEN KWANG-WU Algorithms for Bernoulli numbers and Euler numbers J. Integer Seq. 4 (2001), no. 1, Article 01.1.6, 7 pp. (electronic).Z0973.11021; M2002f:11019 [3] A.K.Kwaśniewski Information on some recent applications of umbral extensions to discrete mathematics to appear in the Proceedings of the International Symposium on Recent Advances in Mathematics and its Applications (ISRAMA 2004) pp. 18-20 December, 2004 Kolkata (Calcutta), INDIA ArXiv: math.CO/0411145 7 Nov 2004 | ||
| December 2004 | Ewa Borak | A generalization and common combinatorial interpretation of binomial & q-binomial Gaussian coefficient and Stirling & q-Stirling numbers coefficients |
|
One presents – following Voigt [1] a simultaneous generalization of binomial, Gaussian and Stirling numbers obtained due to an unified combinatorial interpretation of these as a problem of words. A comparison with the similar extension of binomial, Gaussian and Stirling coefficients due to Konvalina [2,3] is one of the goal of the presentation.
Bibliography [1] Bernd Voigt A common generalization of binomial coefficients, Stirling numbers and Gaussian coefficients Publ. I.R.M.A. Strasbourg, 1984, 229/S–08 Actes 8e Seminaire Lotharingien, p. 87–89 http://www.mat.univie.ac.at/~slc/opapers/s08voigt.pdf [2] J. Konvalina Generalized binomial coefficients and the subset-subspace problem Adv. in Appl. Math. Vol. 21 (1998) : 228-240 [3] J. Konvalina A Unified Interpretation of the Binomial Coefficients, the Stirling Numbers, and the Gaussian Coefficients The American Mathematical Monthly vol. 107, No 10 (2000):901-910 | ||
| December 2004 | Wiesław Bajguz | On Kim`s generalization of sums of powers of consecutive integers formula |
|
Formulas for sum of powers of consecutive numbers in natural way leads to
Bernoulli numbers and Bernoulli polynomials. The generalization of this is
presented following [1], where natural numbers involved in the problem are
replaced by q-integers. Thus sums of powers of consecutive q-numbers are
investigated including the corresponding extension of Bernoulli numbers and
polynomials.
Bibliography [1] Taekyun Kim Sums of powers of consecutive q-integers to appear [2] Yuan-Yuan Shen A note on the sums of powers of consecutive integers Tunghai Science vol. 5, 2003, pp. 101-106 | ||
| listopad 2004 | Wiesław Bajguz | Potęgi kolejnych liczb naturalnych, wielomiany i liczby Bernoulliego |
|
Tematem seminarium będą sumy postaci 1n+2n+
3n+...
+kn, gdzie k,n >0 Formuła na sumy sześcianów (n=3) była znana już około roku 500 n.e. W XII wieku w Bagdadzie i niezależnie w XIII w. W Chinach i Indiach matematycy odkryli zależności pozwalające wyliczać sumy wyższych potęg. Jednak skuteczne metody obliczania tych sum znalazł dopiero Bernoulli (1654-1705). Literatura: [1] D. Bressoud Calculus Before Newton and Leibnitz, Part III, AP Central 7/8/04 [2} Yuan-Yuan Shen A Note on the Sums of Powers of Consecutive Integers, Tunghai Science Vol. 5, July 2003. pp. 101-106 | ||
| październik 2004 | Ewa Krot | O pewnej klasie krat geometrycznych związanych z grupami skończonymi |
|
Niech X={x1,x2,...,xn}, |X|=n
i niech G będzie skończoną grupą multiplikatywną.
Skonstruowana będzie krata częściowych G-partycji zbioru oraz zbadane będą jej właściwości. Pokażę, że jest to krata geometryczna (zupełna, atomowa, semi-modularna). Wyznaczę jej funkcję Mobiusa, liczby Whitney’a oraz wielomian charakterystyczny, a także przedstawię tożsamości wielomianowe analogiczne do tych spełnianych przez liczby Stirlinga drugiego rodzaju (tj. liczby Whitney’a w kracie partycji zbioru -elementowego) .
Literatura: [1] T.A.Dowling: A class of Geometric Lattices Based on Finite Groups, Journal of Combinatorial Theory (B),14(1973)61-86 | ||
| październik 2004 | A.K. Kwaśniewski | Umbral extended Stirling and Bell numbers |
|
One introduces explicit formulas for two kinds of Stirling and Bell numbers umbral
extensions which include all q-extended ones recalled recently by Wagner [2].
The umbral extended correspondents to the famous combinatorial sequences above
proposed by Kwaśniewski are the following: a] GHW (*) originated psi-umbral extensions (announced in [1]) and alternative b] Comtet [3,2] psi-umbral extensions of Stirling and Bell numbers. The corresponding Dobinski formula for a] was already delivered in [1] based on recent (see: [1]) works of the author where – among others -umbral extended Poisson distributions were introduced. (*)Graves C. On the principles which regulate the interchange of symbols in certain symbolic equations Proc. Royal Irish Academy vol. 6 (1853-1857), pp. 144-152 S. Pincherle, U. Amaldi Le operazioni distributive e le loro applicazioni all`analisi, N. Zanichelli , Bologna , 1901 (see also [7,8] - below) Literatura: [01] A.K. Kwasniewski Psi-Poisson, q-Cigler, psi-Dobinski, psi-Rota and psi-coherent states ArXive: math.CO/0403054 v1 2 March 2004 [02] Carl G. Wagner Partition Statistics and q-Bell Numbers (q = -1) Journal of Integer Sequences, Vol. 7 (2004), Article 04.1.1 [03] Comtet L. Nombres dr Stirling generaux et fonctions symmetriques C.R. Acad. Sci. Paris, Series A, 275 (1972):747-750 [04] M. Wachs, D. White p,q Stirling numbers and set partitions Statistics J. Combin. Theory (A) 56 (1991): 27 [05] M. Schork On the combinatorics of normal ordering bosonic operators and deformations of it J. Phys. A: Math. Gen. 36 (2003) 4651-4665 [06] J.Katriel, M. Kibler Normal ordering for deformed boson operators and operator-valued deformed Stirling numbers J. Phys. A: Math. Gen. 5 (1992): 2683-26-91 [07] A.K.Kwaśniewski On Simple Characterisations of Sheffer psi-polynomials and Related Propositions of the Calculus of Sequences, Bull. Soc. Sci. Lett. Lodz; 52, Ser. Rech. Deform. 36 (2002) pp.45-65 ArXiv: math.CO/0312397 [08] A.K.Kwaśniewski Main theorems of extended finite operator calculus Integral Transforms and Special Functions Vol 14, No 6, (2003): 499-516 | ||
| wrzesień 2004 | Ewa Borak | Liczby Whitney’a pierwszego i drugiego rodzaju |
|
Rozważymy trzy ciągi wielomianów bazowych przestrzeni R[x]: ciąg potęg xn,
ciąg potęg ubywających Literatura: [1] Joni S.A., Rota G.-C., Sagan B.: From sets to functions: three elementary examples Discrete Mathematics 37 (1981), 193-202. | ||
| 07-06-2004 | Wiesław Bajguz | Zbiory hybrydowe – czyli zbiory dopuszczające ujemną liczbę elementów |
|
Przy pomocy funkcyj Literatura: [1] Loeb D.E. Sets with Negative Number of Elements Adv. Math. 91 No1 64-74 (1992) [2] Loeb D.E. A generalization of the binomial coefficients Disrete. Mathemetics 105 (1992) pp.143-156 | ||
(*)
rodowód: (przed likwidacją ZMD)
wspomnienie
