Gould's Binomial Summation Logo
Gould's Binomial Summation Logo from Combinatorial Identities

The Online Encyclopedia of Integer Sequences
The On-Line Encyclopedia of Integer Sequences

Cobweb Tiling
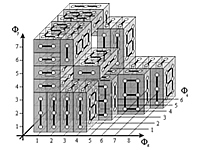
Tiling of hyper boxes

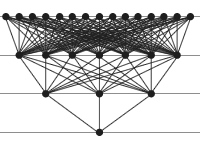
Cobweb Poset of Gaussian integers
Cobweb Poset of Gaussian Integers

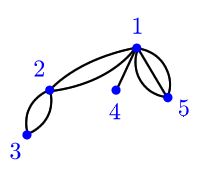
Plane multitree
Plane multitree

Beautiful Julia and Quaternions
Beautiful Julia and Quaternions

Maciej Dziemiańczuk, PhD

University of Gdańsk
Institute of Informatics
Wita Stwosza 57, 80-952 Gdańsk, Poland

Faculty of Mathematics, Physics and Informatics, room 4.23
e-mail: mdziemia at inf.ug.edu.pl

Dyck path

Interests:


For Students (in polish):

Dydaktyka 2021/2022 (semester zimowy):

Konsultacje:

  • Czwartek godz. 14-16 na Wydziale MFI w 4.23 lub na Microsoft Teams w innych porach po wcześniejszym ustaleniu e-mailowo lub bezpośrednio na MS Teams.

Materiały:


Other:

Papers:

  1. B. Wolnik, M. Dziemianczuk, A. Dzedzej, B. De Baets, Reversibility of number-conserving 1D cellular automata: unlocking insights into the dynamics for larger state sets, submitted for publication, 2020.
  2. B. Wolnik, A. Augustynowicz, M. Dziemiańczuk, Bernard De Baets, Reversibility of non-saturated linear cellular automata on finite triangular grids, Chaos 31, 013136, 2021
  3. B. Wolnik, M. Dziemianczuk, B. De Baets, Recurrent Misconceptions in the Study of CA Reversibility on Triangular Grids, International Journal of Bifurcation and Chaos, vol. 31, no. 01, 2150014, 2021.
  4. A. Dzedzej, B. Wolnik, M. Dziemianczuk, A. Nenca, Jan M Baetens and Bernard De Baets, A two-layer representation of four-state reversible number-conserving 2D cellular automata, Journal of Statistical Mechanics: Theory and Experiment, Volume 2019, July 2019.
  5. N. Tuglu, F. Yesil, M. Dziemianczuk, E. Gokcen Kocer, q-Riordan array for q-Pascal matrix and its inverse matrix, Turkish Journal of Mathematics, vol 40, (2016), 1038-1048.
  6. M. Dziemianczuk, On Directed Lattice Paths With Vertical Steps, Discrete Mathematics, vol. 339 (3), pp. 1116-1139, 6 March 2016.
  7. M. Dziemianczuk, Enumerations of Plane Trees with Multiple Edges and Raney Lattice Paths, Discrete Mathematics, vol. 337, pp. 9-24, 28 December 2014.
  8. M. Dziemianczuk, Counting Lattice Paths With Four Types of Steps, Graphs and Combinatorics, vol. 30:6, pp 1427-1452, November 2014.
  9. Naim Tuglu, Fatma Yesil, E. Gokcen Kocer, M. Dziemianczuk, The F-Analogue of Riordan Representation of Pascal Matrices via Fibonomial Coefficients, Journal of Applied Mathematics, vol. 2014, Article ID 841826.
  10. M. Dziemianczuk, A Combinatorial Interpretation of the Lucas-Nomial Coefficients in Terms of Tiling of Rectangular Boxes, JCMCC: vol. 88, pp. 225-235, 2014.
  11. M. Dziemianczuk, Generalizing Delannoy Numbers via Counting Weighted Lattice Paths, INTEGERS: Vol. 13, #A54, 2013.
  12. M. Dziemianczuk, First Remark On A Zeta-Analogue of The Stirling Numbers, INTEGERS: Vol. 11, #A9, 2011.
  13. A. Krzysztof Kwasniewski, M. Dziemianczuk, Cobweb posets - Recent Results, Adv. Stud. Contemp. Math. vol. 16 (2), 2008 (April) pp. 197-218.